Problem of this week(10/16-10/22)
How many ways are there to place $3$ indistinguishable red chips, $3$ indistinguishable blue chips, and $3$ indistinguishable green chips in the triangles of the following figure so that no two chips of the same color are directly adjacent to each other, either vertically or horizontally(two cells consider to be adjacent if they share a common side)?
$\textbf{(A)} ~60\qquad\textbf{(B)} ~84\qquad\textbf{(C)} ~96\qquad\textbf{(D)} ~126\qquad\textbf{(E)} ~144$
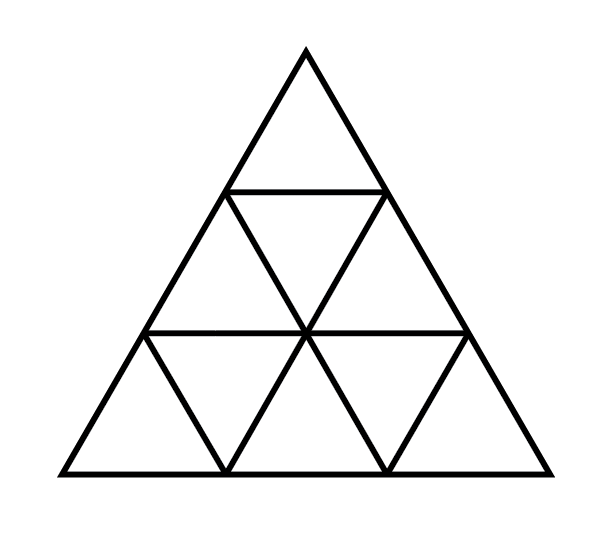

Answer D, 126
Let's label the cells, from top, then left to right, call them $a_1, a_2, a_3, \cdots, a_9$.
Case 1: If the three middle cells $a_3, a_6$, and $ a_8$ are the same color. Then the rest chips can be arbitrary, so for each color, there are 20 ways . for the three colors, this gives 60 ways.
Case 2: $a_3, a_6$ and $a_8$ are not the same, but there are two cells are the same, for example, $a_3, a_6$ are red. $a_8$ are in different color. In this case, the third red can only be in the corner ($a_9$). $a_8$ has two ways to choose a color, once it is fixed, choose any two of $a_1, a_2, a_5$ to be the same will be good. This will give 18 ways. And 18 for blue, 18 for green, so total 54 cases.
Case 3: $a_3, a_6$ and $a_8$ are all different, if $a_3$ is red, then the other two reds have to be either $a_5, a_7$ or $a_7, a_9$, once this is given, everything else is fixed. So there are just two cases, we have 12 cases here,
Add up 60+54+12=126.
Let's label the cells, from top, then left to right, call them $a_1, a_2, a_3, \cdots, a_9$.
Case 1: If the three middle cells $a_3, a_6$, and $ a_8$ are the same color. Then the rest chips can be arbitrary, so for each color, there are 20 ways . for the three colors, this gives 60 ways.
Case 2: $a_3, a_6$ and $a_8$ are not the same, but there are two cells are the same, for example, $a_3, a_6$ are red. $a_8$ are in different color. In this case, the third red can only be in the corner ($a_9$). $a_8$ has two ways to choose a color, once it is fixed, choose any two of $a_1, a_2, a_5$ to be the same will be good. This will give 18 ways. And 18 for blue, 18 for green, so total 54 cases.
Case 3: $a_3, a_6$ and $a_8$ are all different, if $a_3$ is red, then the other two reds have to be either $a_5, a_7$ or $a_7, a_9$, once this is given, everything else is fixed. So there are just two cases, we have 12 cases here,
Add up 60+54+12=126.
AMC 10/12 exam time:
A: Nov. 10, 2022
B: Nov 16, 2022
AMC 8: January, 17-23, 2023
A: Nov. 10, 2022
B: Nov 16, 2022
AMC 8: January, 17-23, 2023
Archive